Am Beispiel der Funktion
	wird eine vollständige Kurvendiskussion durchgeführt :

 
 

1.)	Definitionsbereich
	Der Definitionsbereich umfaßt die Menge aller reellen Zahlen.

 
 

2.)	Symmetrie
	Da die Funktionsgleichung weder nur gerade bzw. ungerade Exponenten von x enthält, ist keine Symmetrie vorhanden.

 
 

3.)	Nullstellen
	Wir erkennen :
	Aus dem zweiten Faktor ergibt sich :
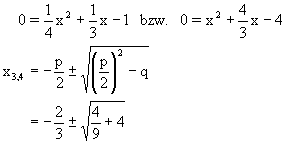	Damit lauten die weiteren Nullstellen :

 
 

4.)	Stetigkeit
	Da es sich bei f(x) um eine ganzrationale Funktion handelt, ist diese im gesamten Definitionsbereich stetig.

 
 

5.)	Extrempunkte
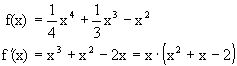	Wir setzen die erste Ableitung gleich Null und lösen die Gleichung :
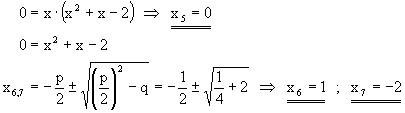	Durch Einsetzen in die Ausgangsgleichung ergeben sich folgende Extrempunkte :
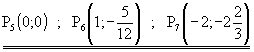	Zwecks Nachweis und Festlegung der Art der Extrema wird die zweite Ableitung untersucht :
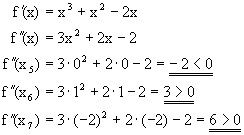	Folglich handelt es sich bei P5 um ein Maximum und bei P6 und P7 um ein Minimum.

 
 

6.)	Wendepunkte
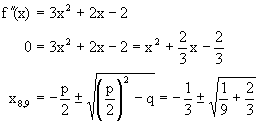	Die Lösungen lauten :
	Wir erhalten die Wendepunkte mit den gerundeten Koordinaten
	Zum Nachweis der tatsächlichen Existenz ist die dritte Ableitung zu untersuchen :
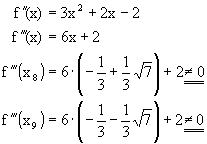	Da die dritten Ableitungen an den Wendestellen von Null verschieden sind, ist die Existenz der Wendepunkte bestätigt.

 
 

7.)	Monotonie
	Aus dem typischen Verlauf einer Funktion vierten Grades und den zuvor berechneten Extremstellen ergibt sich :

 
 

8.)	Wertebereich
	Bei den Untersuchungen im Abschnitt "Extrempunkte" haben wir erkannt, daß der Punkt P7 das absolute Minimum des nach oben geöffneten Funktionsgraphen von f(x) ist. Folglich gilt :

 
 

9.)	Verhalten im Unendlichen
	Bei beidseitig nach oben geöffneten Funktionsgraphen ist zu notieren :

 
 

10.)	Funktionsgraph
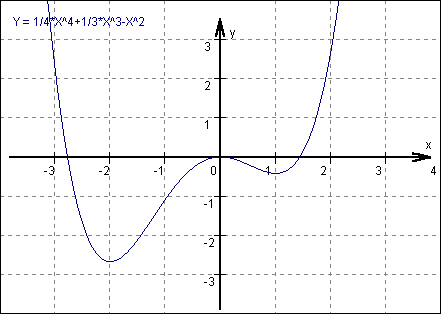